|
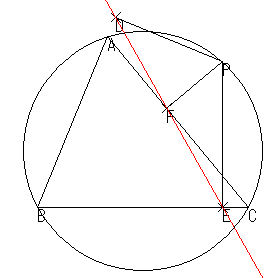
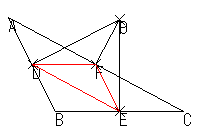
シムソンの定理 ΔABCとその外接円 O がある。円 O 上の点 P から三角形のそれぞれの辺 AB,BC,CA あるいはその延長線上に下ろした垂線の足を D,E,F とするとき,この 3 点は一直線上にある。 この直線を シムソン線と言う。
 |
以下に記述するのは,シムソンの定理の教材化の過程で,私なりに探究した経過です。もちろん,別の展開もありうるでしょうし,既知の内容であることもあるかもしれません。お気づきの点などありましたら,メールをいただければ幸いです。
出発点はシムソンの定理です。つまり
シムソンの定理
ΔABCとその外接円 O がある。円 O 上の点 P から三角形のそれぞれの辺 AB,BC,CA あるいはその延長線上に下ろした垂線の足を D,E,F とするとき,この 3 点は一直線上にある。
この直線を シムソン線と言う。
これを素材にして,いろいろな教材化を行なうなかで,「生徒が調べる課題」にしてみることを試みました。
上の図をただ眺めてもシムソン線のよさは分かりません。上の図の中の点Pを動かしてみると,いつも赤い線が3点を通ることは分かります。しかし,やはりそのよさは分かりにくいままです。そのため,「調べる」ためのよくある手の一つとして,「条件を一般化し,特別な現象として観察する」ようにしてみました。つまり,
問題1
ΔABCと動点Pがある。点 Pから三角形のそれぞれの辺 AB,BC,CA あるいはその延長線上に下ろした垂線の足を D,E,F とするとき,この 3 点が一直線上にあるようにしたい。点Pをどこにとったらいいか。
この問題では,外接円は生徒が発見すべき対象です。いろいろな場所で共線性が成立することを発見し,その点をプロットしていくことによって,発見すべき対象,つまり「OHP作戦」などが使えるような教材化と言えます。
問題1のままでもいいのですが,共線性を発見するときに,「3点のうちの2点を結び,残りの1点がそこを通るかどうか」という設定は,「共線性」を意識し,「調べる課題」に変えるための一つの工夫ではあるのですが,ちょっと違和感があります。「なぜ,一点だけ外しておくのか」そういう感じがします。
そこで,発想をちょっと変えてみて,「つぶれた三角形」として観察できるようにしてみました。つまり,
問題2
ΔABCと動点Pがある。点 Pから三角形のそれぞれの辺 AB,BC,CA あるいはその延長線上に下ろした垂線の足を D,E,F とし,それらを結んでΔDEFを作る。Pの位置を変えるとΔDEFの形も変わる。Pをどこに取るとΔDEFはつぶれてしまうか。
この図も悪くはないのですが,問題文から自然な形で考えると,むしろ「内部」に点があるのが妥当であり,次の形の方が自然と言えます。
問題3
ΔABCと動点Pがある。点 Pから三角形のそれぞれの辺 AB,BC,CA あるいはその延長線上に下ろした垂線の足を D,E,F とし,それらを結んでΔDEFを作る。Pの位置を変えるとΔDEFの形も変わる。Pをどこに取るとΔDEFはつぶれてしまうか。
すると,当然のことですが,内部ではΔDEFはつぶれません。つまり,普通に調べるとつぶれないはずなのだが,あるいは,頂点A,B,CとPを一致させたときだけにつぶれるのだが,外にまで範囲を広げると,外接円を発見する,そういう問題になります。ここで,「外にまで範囲を広げると」ということも重要です。問題2の形で提示すれば,「外もあるんだな」と感じつつ,「なぜこんな場所にあるんだろう」と不自然さを感じます。問題3の形でより自然の内部においておくと「内部だけを調べる」方がある意味で自然ですから,たとえば教室などで,外部まで広げて「あれ」と感じる生徒の存在を想定して,「○○君は面白いことをしている。そういう手もあるか」という流れを作ることが前提となります。
また,内部で動かすのが自然という立場から考えると,「面積0」に注目するよりも,「面積最大」に注目する方が自然です。そういう意味で,次の問題が派生します。
問題4
ΔABCと動点Pがある。点 Pから三角形のそれぞれの辺 AB,BC,CA あるいはその延長線上に下ろした垂線の足を D,E,F とし,それらを結んでΔDEFを作る。Pの位置を変えるとΔDEFの形も変わる。PをΔABCの内部のどこに取るとΔDEFは最大値を取るか。
この問題を考えたときは,「このように考えることも自然になる」という気持ち,つまり問題作りの一つの例として考えていました。たとえば,附属高校の公開授業の前にまとめた公開講座の資料では,そういう一例として挙げています。そして,この時点では,「答えはどうなるか分からない」問題として考えていました。解が存在することは明らかです。しかし,今まで目にした資料の中にはあまり見いだせない問題です。フリーハンドで描いてみてもすぐ答えが分かるような問題ではありません。そういう意味でも,「未解決」あるいは「手をつけていない問題」でした。
1999/11/10の授業に向けて,いくつかの段階を経ておくことが予定されていました。最初の時間では,外心の問題を,教師が提示する1台のパソコン(プロジェクタ)を観察し,議論することに焦点を当てました。11/06の授業では,実際に生徒が操作して調べる課題を行ないました。そして,11/08では,LANでのファイル共有の機能等を使うと同時に,問題3(11/10予定)への伏線として,問題4を扱いました。つまり,点Pを動かしながら,三角形が特別な条件を満たす場合を探すという探究を体験すると同時に,ここでは「最大値」を,そして10日は「最小値」を求めるという流れを構成することにしました。このときは,「図形を動かしながら調べる」という行為をきちんと確認できる問題という意味で,「答えが一つ」になる問題を扱いました。
実は,授業開始時点では,問題の解答が見つかっていないったのですが,授業が進むにつれ,「本当はどうなんだろう」と感じました。授業者もそこはきちんとはわかっていないと言います。「できれば,授業内に解答が得られる方がいいのだし」と思いました。
このときの私の発想と手続きは次の通りです。
すると,驚いたことに外心がその候補になりそうです。簡単な答えはないだろうと予想していたのでびっくりしました。同時に,「この三角形」だけで納得することはできないから,「いろいろな三角形」で調べることが不可欠だと思いました。
「いろいろな三角形」について調べるとき,それぞれの三角形において「最大」ということを確認するのは面倒です。そこで,次のことを考えました。
まず,「面積最大」=「面積比 = 0.25」が確かかどうかを確認しました。
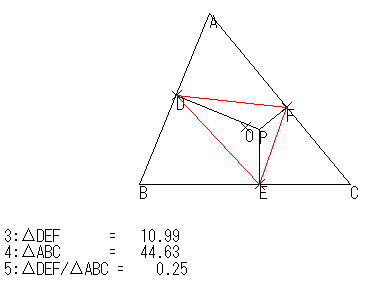
すると,上の図のように,結構離れていても表示は「0.25」になります。「本当か?」と,桁数を増やしてみました。
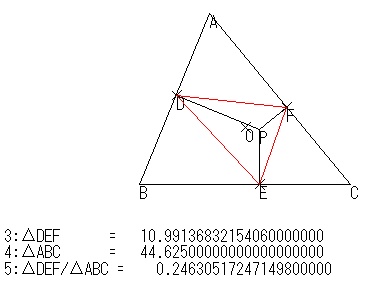
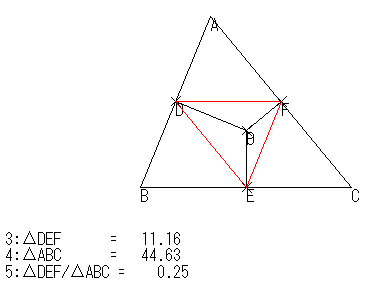
また,Pを外心に一致させてみると,
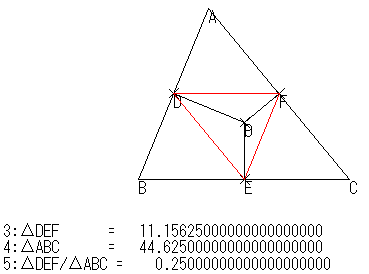
これでかなり確信を得つつ,次の図で点Aを動かしてみました。
すると,次の図にも代表されるように,Aをどこにとってもこの「0.25」という値は保持されます。これによって,「ΔDEFが最大になるのは P が外心のときだ」と実感しました。
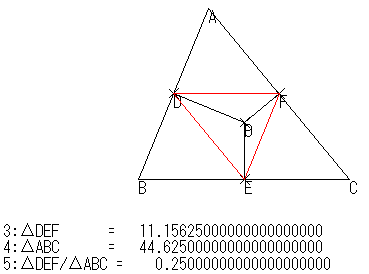
不謹慎と言えば不謹慎な話なのですが,これが分かったのは,授業中でした。授業を参観しながら,空いているパソコンで作業してみて分かったのです。授業者の日下部先生に,「どうも外心みたいだよ」と耳打ちし,授業の流れも臨機応変に変えることにし,「与えた図で大体の場所が分かったら,元の三角形をいろいろな三角形(生徒が作ったものの中には直角三角形や鈍角三角形などがあった)について調べてみて,それらの結果から,この点はどういう点か考えてみよう」という流れにしました。
生徒は「0.25」は使いません。自分が作った三角形について探索的に「面積が最大なところ」を発見し,自分の画面や他の生徒の画面の結果から,「どうもこれは外心らしい」と実感したわけです。
いずれにしても,上記の考察によって,次の命題を見つけることができました。
命題5
ΔABCと動点Pがある。点 Pから三角形のそれぞれの辺 AB,BC,CA あるいはその延長線上に下ろした垂線の足を D,E,F とし,それらを結んでΔDEFを作る。Pの位置を変えるとΔDEFの形も変わる。PがΔABCの内部を動くとき,PがΔABCの外心と一致するときにΔDEFは最大値を取り,その値は(1/4)ΔABCである
証明はしませんでした。というよりも,外心らしいということは実験的には確信持てましたが,証明に関しては授業者も私もまったく手がかりがなかったのです。(今,これを記述している段階でも,証明の手がかりはまだない。)
時間的な順序で言えば,この次に,11/10の附属高校での公開授業に続き,それを話題とした数学科教育CIIの授業と続くのですが,この数学科教育CIIの授業では,「生徒と同じ立場で作業をしてみよう」という流れの中で,11/08の発問も扱ったのですが,そのときに注目すべきことがあったので,まずそれをここに書いておこうと思います。
課題は問題4のままです。私は「Pの位置はどこか」と考え,しかも,ずるいことに「比較の候補として外心,重心,内心,垂心」を考え,「外心と一致する」という観点で探究を進めました。グループごとの作業と発表を念頭に置いたので,「どんな三角形を調べたらよさそうか」という発問に対して提起された「正三角形」,「二等辺三角形」,「直角三角形」,「直角二等辺三角形」,「鈍角三角形」,「鋭角三角形」を調べてもらいました。鈍角三角形に関しては,予想通り,「最大」を三角形内部に限定するか(この場合は,ある辺の中点になる),それとも三角形の外部も考えるか(外部もどこでもいいと考えてしまうと無限に大きくなってしまう)は問題になりましたが,意外だったのは,どのグループも,私とは全く違った観点から,「これは外心だ」ということに気づいたのです。
彼らの図は,次のようなものでした。
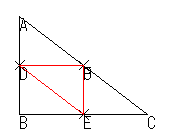
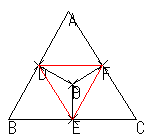
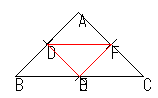
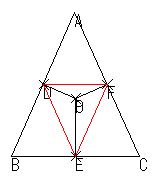
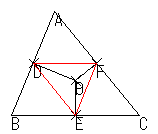
これらの図で彼らが注目したのは点Pの位置ではなく,三角形DEFでした。あるいは,D,E,Fの位置でした。つまり,
という発想です。私は点Pの位置にばかり気を取られていましたが,なるほど,当たり前と言えば当たり前です。そして,外心の場合には面積比が 1/4 になることが当たり前であることがよく分かりました。(1/4 が最大値になることにはまだ遠いですけど)
同じ問題にアプローチする場合にも,目に付けどころも多様なら,それによって気づくこと,「当たり前」と思えることも変わることを実感しました。
さて,時間を元に戻します。11/08の授業はかなり成功したので,11/10の当日の授業はかなり安心していられました。OHPシートを使った授業をするのは初めてでしたが,それもほとんど問題なく使えましたし,また生徒も作業(面積が 0 となる点を見つけ,それをプロットすること)の意図も手順も理解し,結構楽しんで参加してくれました。そして,OHPシートを比較したり,重ねたりしながら,それがΔABCの外接円をなすことを「なるほど」と納得してくれていました。
つまり,このような図を想定していると言っていいでしょう(授業では,外接円は,生徒がプロットした点の集合として プロジェクタで表示され,黒板に,フリーハンドで図が描かれた。
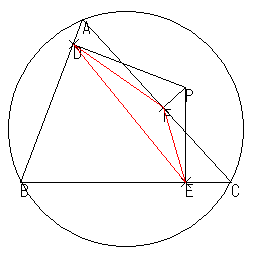
これを見ながら,次のことが思い浮かびました。
公開授業中ではあったのですが,その場で結果を見てみたいという気持ちが強くなりました。まず P を動かして,ΔDEFの変化の様子を観察してみました。「うーん」よく分かりません。同心円になりそうな,そうでないような。そこで,同心円を追加してみました。
半径を変えてみても結果は同じです。つまり,実験的な結果として,次の命題が成立することが分かりました。
命題6
ΔABCの外心Oを中心とする円C上に点Pをとり,それぞれの辺(およびその延長)に下ろした垂線の足をそれぞれ D,E,F とすると,ΔDEFの面積は一定である。
特に,C が外接円に一致する場合には,面積は 0 となる。
また,Cが外接円に含まれるような円のみに限定すると,Pが外心 O と一致する場合は面積が最大になり,ΔABCの1/4となる。
これらの結果は,実験的には正しいことが確証されていますが,現時点でも,その証明は分かっていません。(証明のための模索は,この続きとして書くことになるでしょう。あるいは,別の方が解決する方が早いのかもしれません。ぜひ,チャレンジしてみてください。)
外の三角形と中の三角形の関わりという意味ではある程度単純な形になっているとは言うものの,証明を考える上でちょっと手の出しようがないように思えたので,内外の三角形を別の形に分割し,それらの間に同様の関係性が保持されないかと考えてみた。二種類考えてみたが,うまくいきそうもないので,諦めた。
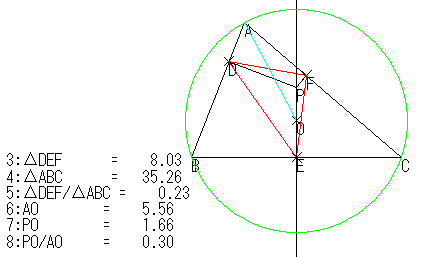
同心円上で面積が一定ということが今まで分かっていたわけだが,その半径と外接円の半径の間にどういう関係があるかを考えてみた。
しかし,これも補助線をいくつか追加してみても分からない。そこで,測定から実験的に推測してみることにした。
測定するのは,AO,POである。
また,そのときの変数として注目しているのが,ΔDEF/ΔABCである。
変化させるのは Pつまり PO なのだが, これが単独で意味があるわけではないので,数式として, 「PO/AO」を作った。
数値の観察だけではこれもよく分からない。そこで,観察した数値を Excel のワークシートの中に手書きで書き込んでみた。
いくつかのデータを元に,散布図を描いてみた。
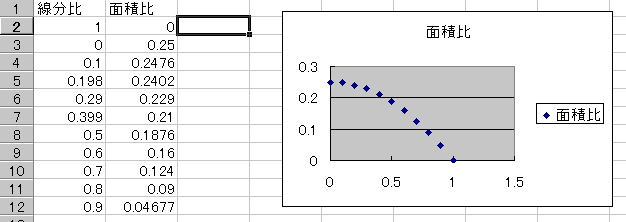
すると,上に凸の2次関数のように見える。
そのため,「(PO/AO)^2」と面積比を変数としてグラフを描いてみた。
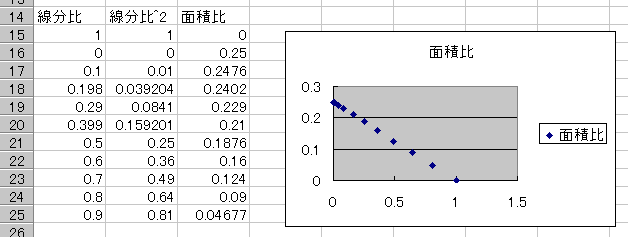
すると,グラフが直線になる。
これを手がかりとして,ΔDEF/ΔABCを PO,AOで表す式を考えてみた。
その結果得られたのが,
これらから,次の命題が得られたことになる。
命題7
ΔABCの外心Oとする。動点Pをとり,それぞれの辺(およびその延長)に下ろした垂線の足をそれぞれ D,E,F とすると,ΔDEFの面積は次の式で表される。
ΔDEF = ΔABC * (1 - (PO/AO)^2)/4
特に,P が外接円にある場合には,面積は 0 となる。
また,P の動きを三角形の内部(等[鈍角三角形の場合は修正が必要])に限定すると,Pが外心 O と一致する場合に面積が最大になり,ΔABCの1/4となる。
もちろん,これらも実験結果からの確証は得られているが,証明は得られていない。
関数関係を見ると,POが重要な役割を負っている。これを使わずに,証明がうまくいくはずはない。そう確信した。
しかし,残念なことに,その希望はすぐに頓挫する。
実際,Pの動きを分かりやすくしようと,BCの垂直二等分線上に制限してみた。
高さをPO等を使って表そうとすれば,DFとPOのなす角が一定等であると便利なのだが,実際には,DFの向きは P の動きと共に変わってしまうのだ。
落胆しながら眺めていると,別のことに気づいた。
ΔDEFの3辺の向きは変化するが,PD,PE,PFの向きは変わらないのである。
つまり,
ΔDEF = ΔPDE + ΔPEF + ΔPFD
と分割してみると,
ΔDEF = {PD・PE sin (∠DPE) + PE・PF sin(∠EPF) + PF・PD sin(∠FPD)}/2
ΔDEF = {PD・PE sin (π - B) + PE・PF sin(π - C ) + PF・PD sin(π - A)}/2
ΔDEF = {PD・PE sin B + PE・PF sin C + PF・PD sin A}/2
という新しい表現が得られた。これはこれで意外な式である。3つの辺への垂線の足と3つの角によって表現されている。頂点と P との距離は直接は関係していない。
そこで,この式から,sin * を消去し,AP等を含むことをもくろんでみたところ,正弦定理を使ってみると,次の式が得られた。
ΔDEF = {PD・PE・DE / BP + PE・PF・EF / CP + PF・PD・FD / AP}/2
式にあまり自信がなかったので,この一部としての
ΔPDF = PF・PD・FD / (2AF)
を確認してみた。
果たして,これらの表現は使い道があるのだろうか。分からない。
より単純化した式としては,次の命題が見つかったともいえるが,やはりこれも証明されていないままである。
命題8
四角形 PABC において, ∠A = ∠ C = ∠ R のとき,
ΔABC = AB・BC・CA /(2 PB)
命題8'
ΔABC の外接円の半径を R とするとき,
ΔABC = AB・BC・CA /(4 R)
なお,関連して,次のような図を作ってみた。
ΔDEFの辺の向きが動いてしまうので,3つの三角形をもとにそれぞれ平行四辺形を構成し,6角形をつくったわけである。
この6角形の面積を S とすると,上記の式から,
S = PD・PE sin B + PE・PF sin C + PF・PD sin A
= PD・PE・DE / BP + PE・PF・EF / CP + PF・PD・FD / AP
となっている。
なお,ΔABCが鋭角三角形,直角三角形の場合,この奇妙な6角形は,PがΔABCの内部にある限り,やはりΔABCの内部に含まれている。
話題が広がってしまったので,元の問題はなんだったっけと振りかえってみた。そして,命題7の図を見直してみると,今までと違う見方をすることができた。
命題8は内側の三角形を3つに分割して見てきたのだが,外側にある3つの三角形にも適用できることと,それらを引くことで,内部の三角形の面積を求められることである。つまり,
ΔADF = AD・DF・FA / (2AP)
ΔBED = BE・ED・DB / (2BP)
ΔCFE = CF・EF・FB / (2CP)
ΔDEF = {ΔABC - (ΔADF + ΔBED + Δ DEF)}
なお,ここで AP,BP,CPに関しては,三平方の定理を使えば,
AP2 = AD2 + DP2
AP2 = AF2 + FP2
*
BP2 = BD2 + DP2
BP2 = BE2 + EP2
*
CP2 = CE2 + EP2
CP2 = CF2 + FP2
が使える。
先が見えなくなってきたので,別の観点から少し調べてみた。
「外心を中心とする円上を P が動いたときの不変量」
の一つとして,
ΔDEFの面積
が見つかったわけだが,他に,同様の不変量がないだろうか
という発想である。
しかし,以下に見るように,いくつか調べてはみたものの,見つからなかった。
いきあたりばったりはだめである。
| 内容 | 結果 | 備考 |
|---|---|---|
| 垂線の足の長さの和 | × | これは線型関数だったかな。 |
| 垂線の足の長さの2乗の和 | × | 有力候補と思ったけど |
| 三角形の周の長さ | × | |
| 三角形の辺の2乗の和 | × | |
| 三辺の中点と垂線の足の差の和 | × | 外心からの垂線の足なので有力と思ったが |
| 三辺の中点と垂線の足の差の2乗の和 | × | 同上 |
| 各頂点との距離の和 | × | これはフェルマー点だった |
| 各頂点との距離のの2乗の和 | × | これは重心だった |
まあ,なぐさめとしては,命題6や命題7は,ある意味では珍しい不変量あるいは関数関係を見つけたということになるということだろうか。
なかなからちがあかない状態になってしまったので, まず, gc-mlとNekokidsに投稿してみた。しかし,反応がないので,続いて matheduに投稿してみた。そこでいろいろな反応があり,新たな展開を得ることになった。続きはこちら