問題状況
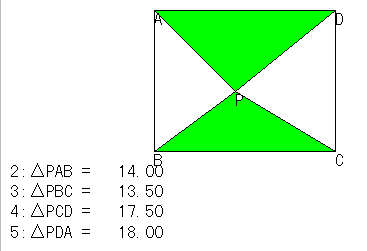
四角形ABCDと動点 P がある。
S1=ΔPAB+ΔPCD
S2=ΔPBC+ΔPDA
とするとき,S1=S2となるような点 P の位置を調べたい。
どんな四角形のときに,どんな結果になるか。
[数式を組み込んであり,A,B,C,D,Pが動くもの]

川崎市の研究(1999)の中で,この課題で期待できる数学的経験の中に,
条件の多い特殊な場合についてみつけた定理を,「より高い立場」から見直し,統合していく活動が経験できる。という記述がある。大学院の授業で,「これはどういう意味か具体的に説明してみよう」という問いかけをしたが,あまりいい返事がなかった(1999/11/12)。
点Pが内部から外部に移動すると,「和」としての等式は成り立たなくなる。しかし,大きい方から小さい方を引いた値としての「差」に注目すると,成り立つようになる。川崎市の研究(1999)では,「〜」という記号で表現されているが,「和あるいは差」として成立する式,あるいは,面積に正負を含めて考えた場合の和を考えると,「内部」のみでなく,「どの点でも」成立すると解釈することができる。
以下は,そのような観点から,面積(+/-)で作図したものである。
長方形でうまくいくということの証明を次の図で考えていたとする。
これを平行四辺形に一般化するときに,どう考えたらいいのか。
たとえば,一つの考えとしては,次のものがある。
しかし,考えにくい。むしろ,「水平と垂直」にこだわるよりも,「辺に平行」に観点を移して,次のように考えた方がすっきりするし,アイデアもそのまま移行する。
平行四辺形では「内部の(あるいは平面内の)すべての点」で成立する。それに対して,台形では,ある直線上でしか成立しない。

この「直線」の特徴づけをどう考えたらいいか。
最も基本的なのは,
「平行でない2辺の中点を結んだ直線」であろう。
あるいは,
「平行線から等距離にある点の集合」という見方もあるだろう。
この見方をしたときには,平行四辺形と台形の関わりはあまり明確ではない。
「台形」に関して,このような見方をしたとき,
「平行でない」はナンセンスだ。
また,「平行線から等距離にある点の集合」と考えた場合には,
次のように,「2直線」が浮かび上がるが,それがどういう意味があるのかはよく分からない。

むしろ,考えやすいのは,
「平行四辺形は 2組の平行性があるので,2次元」
「台形は 1組の平行性があるので 1次元」
という見方ではないだろうか。
(ここから「一般の四角形は 0次元(点)」と推測すると,実は正しくない。
上記のように,「一般の四角形は 0次元(点)」と推測すると,実は正しくない。つまり,やはり直線になる。この直線は,「対角線の中点(2つある)を結んだ直線」である。
この見方をすると,「台形」はやはり,対角線の中点を結んだ直線」と見直すことができる。
一般の四角形はどうなるだろうか。実は,GCを使うと,次のような画面となってしまう。
「すべての点」でいいはずなのに,「消えてしまった」。
実は,これは作図ツールの性格上,仕方がないことなのだが,「異なる2点」を通るものとして,直線を作図しているのだが,ここでは「2点が重複してしまった」から「消えてしまっている」。むしろ,「2点を通る直線」は,「1点を通る直線」で十分なため,対角線の交点を通るすべての直線上の点,つまり平面上の点すべてで成立することを意味する。
上記で一応終わりと考えてもいいのだが,さらに「2n角形」に一般化を試みるような場合は,やはり直線が登場するため,「なぜだろう」という疑問が生じてくる。
次のような見方をしてみることにする。
S1(P) = S11(P)+S12(P)
S2(P) = S21(P)+S22(P)
ここで,
S11は上の三角形の面積,S12は下の三角形の面積である。
S21は左の三角形の面積,S22は右の三角形の面積である。
三角形の面積が底辺×高さ/2であることを考えると,
たとえば,Pがある一直線上を動いたとき,それぞれが1次関数になることが分かる。
すると,1次関数の和であるから,S1,S2も1次関数である。
たとえば, S1が同じ値を取るような異なる2点が見つかった場合,その2点を通る直線上では定数になる。
これは三角形をいくつ足しても同じである。つまり,4角形に関することを 2n角形に一般化したとしても,まったく同じことが成立することになる。
S1とS2を考える場合, 2n 角形に関しては等しくならない場合もありうる。両方が異なる定数となる場合にはありえない。しかし,S1,S2のそれぞれに関しては「等高線」がありうる。両方の等高線の在り方を比較した場合,その構造が全く同じになっているときが「平面全体」。構造が同じで値がずれているときが「ない」。そして,一般の場合は,二つの構造(それぞれが3次元グラフの中での平面となるので)の交わりとしての「直線」となっていることが分かる。
さて,このように本質的にこの問題の背景にあるのは線型関数である。このことを踏まえると,「台形が1本で平行四辺形が2本ということと,直線,平面全体」との関わりが見えてくる。つまり,それらは解集合の「基底」なのである。それらがなす1次結合全体の集合が解集合になるため,「2本」ある場合には,その2本のベクトルによって生成される平面全体が解になるということだったのだ。