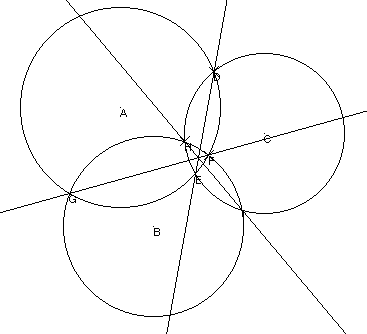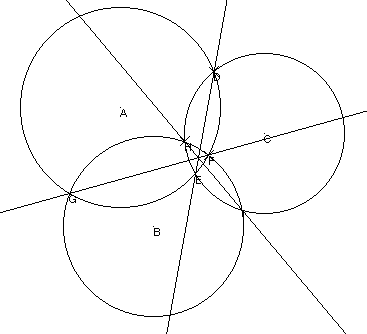3円交線の証明(相似の伝染)


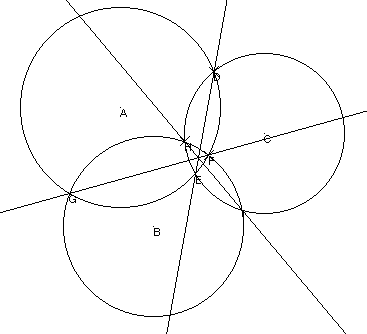
元の問題

3つの円がある。
それぞれの2つずつの円に注目し,交点を通る直線を引いてみるとそれらの3つの直線が一点で交わることを証明せよ。

アイデア

条件のうちの2つの円だけを使って図を作る。そこで2組の相似な三角形があれば,もう一つも相似になってしまうことを述べる。そして,もう一つの条件が満たされてしまうことを述べる。

補題:

交わる2つの円がある。それぞれの円の一つずつの弦と交点を結ぶ弦が共点であるとき,二つの弦は同一円周上にある。

補題を利用した元の問題の証明

次の図の流れを見て,考えてみてください。

3つの円を元にして,一部の点と直線を使います。


元の円と使わないものはいったん消しておきましょう。




補題を使うと4点は円を通ることになります。


さて,新しくできた円は,「元の円」と一致します。
(3点を共有するから)
つまり,元の3つの円を使って作図しても,3つの弦は「共点」 になります。

補題の証明のための図の構成

まず,A,Bを中心とする2円があり,その交点をC,Dとする。
次に,図のように,円A上にE,Fがあり,CDとEFの交点をXとする。
また,円B上に点Gがあり,GXの延長と円Bとの交点をHとする。

(作図の仕方としては,E,G,Xを基に,F,Hを構成するのでもよい)

さらに,次の図のように,6つの線分を追加する。



すると,
になる。(対頂角と円周角による)

そして,さらに,
になる。



よって,∠EHG = ∠EFG となるので,
E,H,F,Gは同一円周上にある。
つまり,