「相似性」が成立するような一般化の限界

- 「２辺正３角」の一般化 -

愛知教育大学　数学教室
飯島康之

元の問題状況

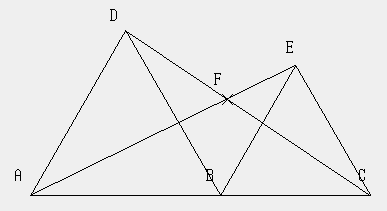
辺AC上に点Bを取る。AB と BC をそれぞれ一辺とする正三角形 ABD と BCE を線分 AC に対して, 同じ側に作る。
そして, DC と AE の交点を F とする。

考察のきっかけ

この考察のきっかけは,福井県大野市の廣瀬先生からの提案です。生徒に一般化のプロセスを経験させる上で,どういうワークシートを作ったらいいだろうか, こういうのはどうだろうかという議論の中で,「相似な三角形」まで発展させたいという提案がありました。
実は,私はそのとき,その意図が分かりませんでした。この教材は,一般的には,二つの合同な三角形の組が残るような一般化までを扱うのが普通です。そして,そのためには,二組の辺が等しいことが必要であり,たとえば,頂点を共有する二等辺三角形あるいは,それを一部と持つような相似な図形まで一般化するのが普通です。相似な一般の三角形に持っていったとしても,それはうまくいかないのではないかと思いました。

しかし,実際には,そんなことはなかったのです。それを,別の観点から,WWW上でまとめてみたのが,これです。

相似性のみならば,どういう性質が生き残るか

この図においては, ΔABEとΔDBCが合同です。そして,合同性を保つような一般化の限界は,上記に述べたようなことです。
そのときには,
AE = DC , ∠AFC = 120°(一定)
などが成立します。
ここで,合同ではなく,相似であればいいと条件を緩めるとどうなるでしょう。

まず, AE = DC のような,長さに関する性質は生き残れません。
また, ∠AFCなども,その大きさがある値になるという性質は生き残れません。
しかし, ∠ EAB = ∠ DBC のような, 角の相等性は生き残ります。
そのため,想定している角が変化してしまうような場合には, 変化しつつも,ある角とある角は実は等しいという現象になりますが,その想定している角が変化しない場合には,ある角の大きさが一定,つまり,ある点の軌跡が円になるという現象は生じます。

つまり, 元の問題状況における特色を

という面でとらえた場合,前者は生き残れないが,後者は生き残れるような一般化を考えることができるわけです。
そういう意味で,廣瀬先生の指摘には,「一本取られたなあ」と,脱帽しました。

図の例

ここでは,その図の例を挙げておきましょう。
どの点を動かすとナンセンスか,どの点を動かすと軌跡が面白いのか等を調べてみてください。